|

Deductive logical reasoning is
a basic form of
valid logical reasoning.
Deductive logical reasoning,
deduction, starts out with a
general statement, or hypothesis, and
examines possibilities to reach a specific, logical conclusion.
In deductive inference, we
go from the general to the specific.
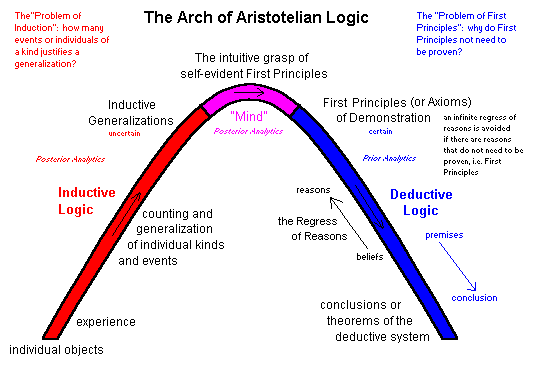
Inductive logical reasoning is the opposite of
deductive logical reasoning.
Inductive reasoning makes broad
generalizations from specific observations.
In inductive inference, we go from the specific
to the general.
Inductive or deductive inference;
observation until a pattern is
discerned.
Now we infer a generalization as an explanation,
hypothesis or theory.
Inference in logic is:
- a proposition reached by
a process of inference from
an
assumption.
- the process of deriving
logical
consequences of that assumption.
- the process of
deducing the fallacies of making
such an assumption.
 Due to the truth of the
preceding statement it is imperative that pattern matches be based on a logic
accurate assessment of reality including an accurate unbiased understanding of
the world outside of personal experience.
Due to the truth of the
preceding statement it is imperative that pattern matches be based on a logic
accurate assessment of reality including an accurate unbiased understanding of
the world outside of personal experience.
Subscription to a belief system
disallows thinking in a rational logic manner.
Anyone who tries to convince you a
belief system will save you is a snake.
Honest rational logical thought requires
the
sacrifice of SACRED COWS !!!

The
Law of Non-Contradiction states that
no statement
(proposition, assertion, etc.) can be
both true and not true
(false).
The Law of Excluded
Middle is generally given as "A is B or A is not B;"
object (A) either
has or lacks a given property (B).
An alternate formulation of this
(with propositions instead of objects) is "p or not p" - but not both.
"There is nothing between asserting and denying." -
Aristotle
The
Law of Identity states that A equals A or "if
any statement is true, then this statement is true."
The
Law of Rational Inference monitors
inferences between premises and conclusions.
If A equals B, and B
equals C, then A equals C.
"The law of rational inference teaches if
premise A and B are valid, then, by what
Martin Luther called
resistless logic, conclusion C follows." - Matthew

Logic is defined herein
as:
A system of valid
reasoning.
The branch of philosophy that
analyzes
inference.
The principles that guide reasoning within
a given field of inquiry.
The
nonarithmetic operations performed by a computer, such as sorting, comparing,
and matching, that involve yes-no decisions.
A branch of philosophy that
deals with the formal principles, methods and criteria of
validity of inference, reasoning
and knowledge.
Logic, concerned with the study of the principles of
reasoning, examines the structure of a statement as distinguished from the
content of a statement.
Logic attempts exact reasoning through formal
thought systems.
Symbolic logic, a meta-language concerned with truth,
represents logical expressions through the use of symbols and
variables.
Propositional logic, also known as sentential logic and
statement logic, is the branch of logic that studies ways of joining and/or
modifying propositions,
statements or sentences to form more complex propositions, statements or
sentences, as well as logical relationships and properties derived from
conjunction.
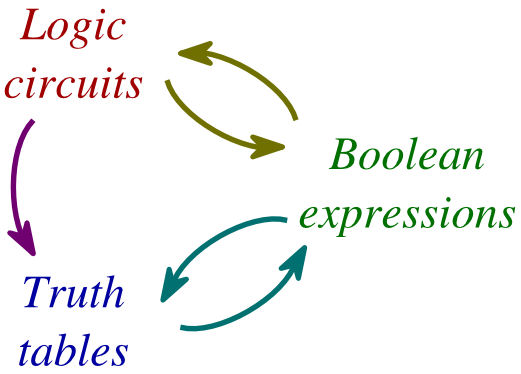
Boolian logic deals with the basic operations of truth
values: AND, OR, NOT and combinations thereof resulting in either a true or
false answer.
Boolean logic is important for computer science because
it fits nicely with the binary numbering system, in which each bit has a value
of either 1 or 0.

Predicate logic contains the
elements of propositional logic, propositional variables and constants, but
adds predicates and quantifiers.
Symbols, typically used in place of
nouns and pro-nouns, are combined into sentences by means of predicates.
The rules of natural deduction describe how we may proceed from valid
premises to valid conclusions, where the premises and conclusions are
expressions in predicate logic.
The syntax determines which
collections of symbols are legal
expressions while the semantics determine the meanings behind these
expressions.
Predicate logic, first-order logic, is completely formal so
that it can be mechanically determined whether a given expression is true or
legal.

modal logic
Modal logic is a type of formal logic primarily developed in the
1960s that extends classical propositional and predicate logic to include
operators expressing modality.
A modal is a word that expresses a
modality which qualifies a statement.
Aristotle tutored
Alexander III in modalities with
syllogisms.

This text will only be understood
only by someone who can follow a thread.
This text deals with philosophy:
the logic of language is misunderstood.
This text might be summed up in
the following two sentences:
What
can be said at all can be said clearly.
What we cannot talk
about we must pass over in
silence.
The aim
of this text is to reveal limits to the expression of
thought.
(Although what can be said
may be stated clearly and succinctly
many times
it is NOT in the interest of
the speaker or writer to do so.
In the case of
propaganda and
deception -
imperative.
To discern pr☠paganda one must follow the logical
thought thread of the proposition being presented.
This edited version
of Tractatus Logico-Philosophicus is an attempt to show one logical thought
thread in the Labyrinth of
the Akashic Records.
All numbering and thoughts by Ludwig
Wittgenstein.
Some dead ends of the logical thought thread of the
Labyrinth of Ludwig, also known as rabbit holes, have been omitted for the sake
of clearity and brevity.)


2
|
In logic nothing
is accidental.
|
2.01
|
We are quite
unable to imagine spatial objects
outside space or temporal objects outside time.
|
2.03
|
In relationships
objects are causually linked to one another like the
links of a
chain.
|
2.04
|
In relationships
objects stand in a determinate relation to one another.
|
2.05
|
The totality of
existing relationships of objects comprises reality.
|
2.12
|
An image is a
model of reality - a snapshot of reality.
|
2.18
|
What any image,
of whatever form, must have in common with reality, in order to be able to
depict reality – correctly or incorrectly – in any way at all, is
logical form, i.e. the form of reality.
|
2.19
|
Logical images
can depict reality.
|


| 4 |
A thought is
a statement.
|
| 4.001 |
The totality of statements is
language.
|
4.021
|
Man possesses
the ability to construct languages capable of expressing materially related
thoughts, without having any idea
how each word has meaning or what its meaning is.
Everyday language is
a part of the human organism and is no less complicated.
It is not
humanly possible to grasp immediately the logic of a language.
Language disguises thought.
Outward form of language
does not infer the form of the thought beneath
as
its outward form is not
designed to reveal the form of the thought.
|
4.003
|
Philosophers arise
during a cultural wide
logic failure.
|
4.01
|
A statement is
an image of reality -
a model of reality as we
imagine it.
A gramophone record, the musical idea, the written notes,
and the sound-waves, all stand in the same internal relation of depicting
knowledge that holds between language and culture.
They are all
constructed according to a common logical
pattern.
|
4.02
|
We understand
the sense of a statement without it having been explained in detail through
a commonly held logic of
depiction.
A statement, an image of
reality, restricts reality to two alternatives: true or false.
In order
to do that, it must chronicle reality
completely.
A statement constructs a reality with the help of a logical
scaffolding, so that one can actually see from the statement how everything
stands logically if the statement is true.
To recognize the truth of a
true statement is to logically understand reality.
When translating one
language into another, translators do not proceed by translating each statement
of the one into a statement of the other, but merely by translating the
constituents of statements. Therefore all
translations will be
corrupt.
The meanings of simple symbols (words) must be explained to us
or defined for us if we are to fully understand them.
|
4.03
|
A statement must use common expressions to communicate
situation.
Only in so far as a statement is logically articulated
that it is an image of a situation.
A statement can be true or false
only if it attempts to be an image of reality.
|
4.1
|
Statements
represent the actuality of states of
affairs.
|
4.11
|
Philosophy aims at the
logical clarification of thoughts.
|
4.112
|
Philosophy is not a body of
doctrine but an activity.
A philosophical work consists
essentially of elucidations.
Philosophy is the
clarification of actual statements.
Without philosophy thoughts are
cloudy and indistinct:
Sophia's task is to make them clear and to
give them sharp boundaries.
Philosophy
defines the limits to the sphere of natural science.
Philosophy
defines the limits to what can be thought and what cannot be
thought.
Philosophy will verify what cannot be said, by presenting
clearly what can be said.
Everything that can be thought at all can be
thought clearly.
Everything that can be put into words can be put
clearly into words.
|
4.12
|
Statements can represent reality, but they cannot represent
the logical form of
reality.
In order to be able to represent the logical form of
reality with statements, we have to be
able to station ourselves as observers somewhere outside logic,
outside
reality.
|
4.121
|
Statements do not represent the logical form of
reality.
The logical form of
reality is mirrored in statements.
Statements reveal
the logical form of
reality.
|
4.21
|
Elementary statement, asserts the existence of
a state of affairs.
If a
statement is elementary there can be no elementary statement contradicting
it.
An elementary statement consists of names. It is a nexus, a
concatenation, of names.
It is only in the nexus of an elementary
statement that a name occurs in a statement.
If
an elementary statement is
true,
the state of affairs
exists.
If an elementary
statement is false, the state of
affairs does not exist.
|
| 4.46 |
Among the possible groups of truth-conditions of elementary
statements there are two extreme cases.
If the statement is true for
all the possibilities then truth-conditions are
tautological.
If the statement is false for all the possibilities
then truth-conditions are contradictory.
In the first case
we call the statement a
tautology; in the
second, a contradiction.
|
| 4.461 |
Statements show what they
say; tautologies and contradictions show that they say nothing.
A
tautology is unconditionally true and
a contradiction is
true on no condition.
Tautologies and contradictions are part of the
symbolism of language, much
as '0' is part of the symbolism of arithmetic.
Tautologies and
contradictions are not images of reality.
The former admit all
possible situations, and latter none.
A tautology
does not stand in any
representational relation to reality
A tautology leaves open to
reality the whole of logical space.
A contradiction fills the whole of
logical space leaving no point in logical space for reality.
Tautologies
and contradictions are thus unable to determine reality in any
way.
|
| 4.464 |
A tautology's
truth is certain, a statement's
possible, a contradiction's
impossible.
Certain,
possible,
impossible:
the first indication of a scale to
be used in the theory of
probability.
|
| 4.465 |
The logical
product of a tautology and a statement says the same thing as the statement.
This product, therefore, is identical with the statement.
It is impossible to alter what is
essential to a symbol without altering its essence.
|
| 4.5 |
What is essential in the most general propositional form must be
included in its description.
The existence of a general propositional
form is proven by the fact that there cannot be a statement whose form could
not have been foreseen.
The general form of a statement
is: This is how things
stand.
|
4.51
|
If
I possess a basic truthful
understanding of all elementary statements then
I can construct a definition of the limits
of the language pattern's ability to define reality
accurately.
|


6.1
|
The statements
of logic must be tautologies.
|
6.112
|
Statements of
logic must be assigned a
unique status among all statements.
Logical statements must be
recognized as true immedialtely through the statement alone.
The truth
or falsity of non-logical statements cannot be recognized from the statements
alone.
|
6.12
|
It is clear
that one could achieve the same purpose by using contradictions instead of
tautologies.
The statements of logic describe the scaffolding of
reality, or rather they represent it.
|
6.124
|
If we know the
logical syntax of a language,
then we have all the statements of logic.
Thus there can be
no surprises in
logic.
In logic process and result are equivalent. (Hence
the absence of
surprise.)
Proof in logic is merely to
recognize tautologies in complicated
cases.
|
6.13
|
Logic is not a body of doctrine, but
a mirror-image of
reality.
Logic is
transcendental.
Mathematics is a logical
method.
|
6.2
|
The statements
of mathematics are equations, and therefore pseudo-statements.
We make use of mathematical statements as inferences or models of
reality.
('What do we actually use this word or this statement
for?' leads to valuable
insights.)
The logic of reality, tautologies in statements of
logic, appears in mathematical equations.
Mathematics arrives at
equations through the method of symbol substitution.
|
6.3
|
The exploration
of logic means the exploration of everything that is subject to law.
Outside logic, or law, everything is
accidental.
|
6.31
|
The
mathematical law of induction cannot possibly be a law of
logic, since it is obviously a statement with sense. - Nor, therefore, can it
be an a priori law.
|
6.32
|
The
law
of causality is not a law but the form of a law.
{"All actions are caused by entities. The nature of an
action is caused and determined by the nature of the entities that act; a thing
cannot act in contradiction to its nature."- Ayn Rand
"If one
thing the same in nature at different times, or two things the same in nature,
are to act in situations the same in their nature, they must act on both
occasions in the same way."- HW B. Joseph}
|
6.33
|
We do not have
an a priori understanding
of the law of conservation, but rather
a priori knowledge of the
possibility of its logical form.
|
6.34
|
All such
statements, including the
principle of sufficient reason,
the laws of continuity
in nature and of
least effort in nature - are a priori insights about the
forms of the statements of science.
|
6.341
|
Newtonian mechanics, for example,
imposes a unified form on the description of
reality.
|
6.342
|
Describing reality by means of Newtonian mechanics
tells us nothing about reality: what it
does tell us about reality is the precise way it is possible to describe
reality by these means.
|
6.36
|
A law of
causality might be termed in the following way:
There are
Laws of Nature.
|
6.362
|
The procedure of
induction consists in accepting as true the simplest law that can be reconciled
with our experiences. Occam's
Razor suggests this.
Using
Occam's Razor rentlessly has
no logical justification,
only a psychological one.
It is clear that there are no grounds for
believing that the simplest eventuality will in fact be realized as a belief
does not declare actuality.
We will see the sun will rise tomorrow?
We do not know whether we will see it rise.
Will we be standing there alive to
witness the sun emerging over the horizon?
|
6.375
|
If only logical necessity exists, then
the only impossibility that
exists is logical
impossibility.
|
6.3751
|
For example, the
simultaneous presence of two
colors at the same place in the visual field is impossible, in fact
logically impossible,
since it is ruled out by the
logical structure of
color.
|
6.4
|
An understanding of Яeality must
lie outside reality.
|
6.41
|
In reality everything is as it
is, and everything happens as it does
happen.
|
6.43
|
The reality of the happy man is
a different one from the reality of the unhappy man.
Death is not an
event in life: we do not live to experience death.
If we take
eternity to mean timelessness,
then eternal life belongs to those who
live in the present.
|
6.44
|
It is not how things are in reality that is
mystical, but that reality
actually exists.
|
6.5
|
When the answer cannot be put into
words, neither can the question be put
into words.
|
6.51
|
Skepticism is
not irrefutable, but obviously nonsensical,
when it tries to raise doubts
where no questions can be asked. For doubt can exist only where a question
exists, a question only where an answer exists, and an answer only
where something can be
said.
Trendy Skepticism : The Badge of The Emotionally Unfit &
Intellectually Bankrupt
|
6.52
|
Even when all
possible scientific questions have been answered,
the problems of life remain completely
untouched. Of course there are then
no questions left, and this itself is the answer.
|
6.521
|
The solution of the problem of life is seen
in the vanishing of the problem.
|
6.522
|
Is not this the reason why those who
have found after a long period of doubt that the sense of life became clear to
them have then been unable to say what constituted that
sense?
|
6.523
|
There are,
indeed, things that cannot be put into words.
They make themselves
manifest. They are what is mystical.
|
7
|
What we cannot
speak about we must pass over in silence.
|

Weltanschauung is the
concept that all ideologies or belief systems - variations on rational logical
systems of thought - are limited and defined by the schemata of common
linguistic understanding - they are
conditional
truths.
"There is no such thing as absolute truth in logic and
mathmatics.
The best that one can do is talk of the truth of statements
given a set of rules of reasoning.
It is quite possible to
have statements that are true in one logical system but false in another."
- John D. Barrow
"Mathematics
is inadequate to describe the
universe, since mathematics is an
abstraction from
natural phenomena." - Ludovico delle
Colombe

|
|
 |
This web site is not a commercial web site and
is presented for educational purposes only.

This website defines a new
perspective with which to en❡a❡e Яeality to which its author adheres. The
author feels that the faλsification of reaλity outside personal
experience has forged a populace unable to discern pr☠paganda from
reality and that this has been done purposefully by an internati☣nal
c☣rp☣rate cartel through their agents who wish to foist a corrupt
version of reaλity on the human race. Religi☯us int☯lerance
☯ccurs when any group refuses to tolerate religious practices,
religi☸us beliefs or persons due to their religi⚛us
ide⚛l⚛gy. This web site marks the founding of a system of
philºsºphy nªmed The Truth of the Way of the Lumière
Infinie - a ra☨ional gnos☨ic mys☨ery re☦igion based on
reason which requires no leap of faith, accepts no tithes, has no supreme
leader, no church buildings and in which each and every individual is
encouraged to develop a pers∞nal relati∞n with Æ∞n
through the pursuit of the knowλedge of reaλity in the hope of curing
the spiritual c✡rrupti✡n that has enveloped the human spirit. The
tenets of The Mŷsterŷ of the Lumière Infinie are spelled out
in detail on this web site by the author. Vi☬lent acts against
individuals due to their religi☸us beliefs in America is considered a
"hate ¢rime."
This web site in no way c☬nd☬nes
vi☬lence. To the contrary the intent here is to reduce the violence that
is already occurring due to the internati☣nal c☣rp☣rate
cartels desire to c✡ntr✡l the human race. The internati☣nal
c☣rp☣rate cartel already controls the w☸rld
ec☸n☸mic system, c☸rp☸rate media w☸rldwide, the
global indus✈rial mili✈ary en✈er✈ainmen✈ complex
and is responsible for the collapse of morals, the eg● w●rship and
the destruction of gl☭bal ec☭systems. Civilization is based on
coöperation. Coöperation with bi☣hazards of a
gun.
American social mores and values have declined precipitously over
the last century as the corrupt international cartel has garnered more and more
power. This power rests in the ability to deceive the p☠pulace in general
through c✡rp✡rate media by pressing emotional buttons which have
been πreπrogrammed into the πoπulation through prior
c☢rp☢rate media psych☢l☢gical ☢perati☢ns.
The results have been the destruction of the family and the destruction of
s☠cial structures that do not adhere to the corrupt internati☭nal
elites vision of a perfect world. Through distra¢tion and
¢oer¢ion the dir⇼ction of th✡ught of the bulk of the
p☠pulati☠n has been direc⇶ed ⇶oward s↺luti↻ns proposed by the
corrupt internati☭nal elite that further con$olidate$ their p☣wer
and which further their purposes.
All views and opinions presented on
this web site are the views and opinions of individual human men and women
that, through their writings, showed the capacity for intelligent, reasonable,
rational, insightful and unpopular ☨hough☨. All factual information presented
on this web site is believed to be true and accurate and is presented as
originally presented in print media which may or may not have originally
presented the facts truthfully. Øpinion and ☨hough☨s have been
adapted, edited, corrected, redacted, combined, added to, re-edited and
re-corrected as nearly all opinion and ☨hough☨ has been throughout time but has
been done so in the spirit of the original writer with the intent of making his
or her ☨hough☨s and opinions clearer and relevant to the reader in the present
time.
Fair Use Notice

This site may contain
copyrighted material the use of which has not always been specifically
authorized by the copyright owner. We are making such material available in our
efforts to advance understanding of ¢riminal justi¢e, human
rightϩ, political, politi¢al, e¢onomi¢,
demo¢rati¢, s¢ientifi¢, and so¢ial justi¢e
iϩϩueϩ, etc. We believe this constitutes a 'fair use' of any
such copyrighted material as provided for in section 107 of the US Copyright
Law. In accordance with Title 17 U.S.C. Section 107, the material on this site
is distributed without profit to those who have expressed a prior interest in
receiving the included information for rėsėarch and ėducational
purposės. For more information see:
www.law.cornell.edu/uscode/17/107.shtml. If you wish to use copyrighted
material from this site for purposes of your own that go beyond 'fair use', you
must obtain permission from the copyright owner. |
 Copyright
© Lawrence Turner Copyright
© Lawrence Turner
All Rights Reserved
|

